🟡 Deflated Continuation in the Carrier Problem

In this example, we study the following singular perturbation problem:

\[\epsilon^{2} y^{\prime \prime}+2\left(1-x^{2}\right) y+y^{2}=1, \quad y(-1)=y(1)=0\tag{E}.\]

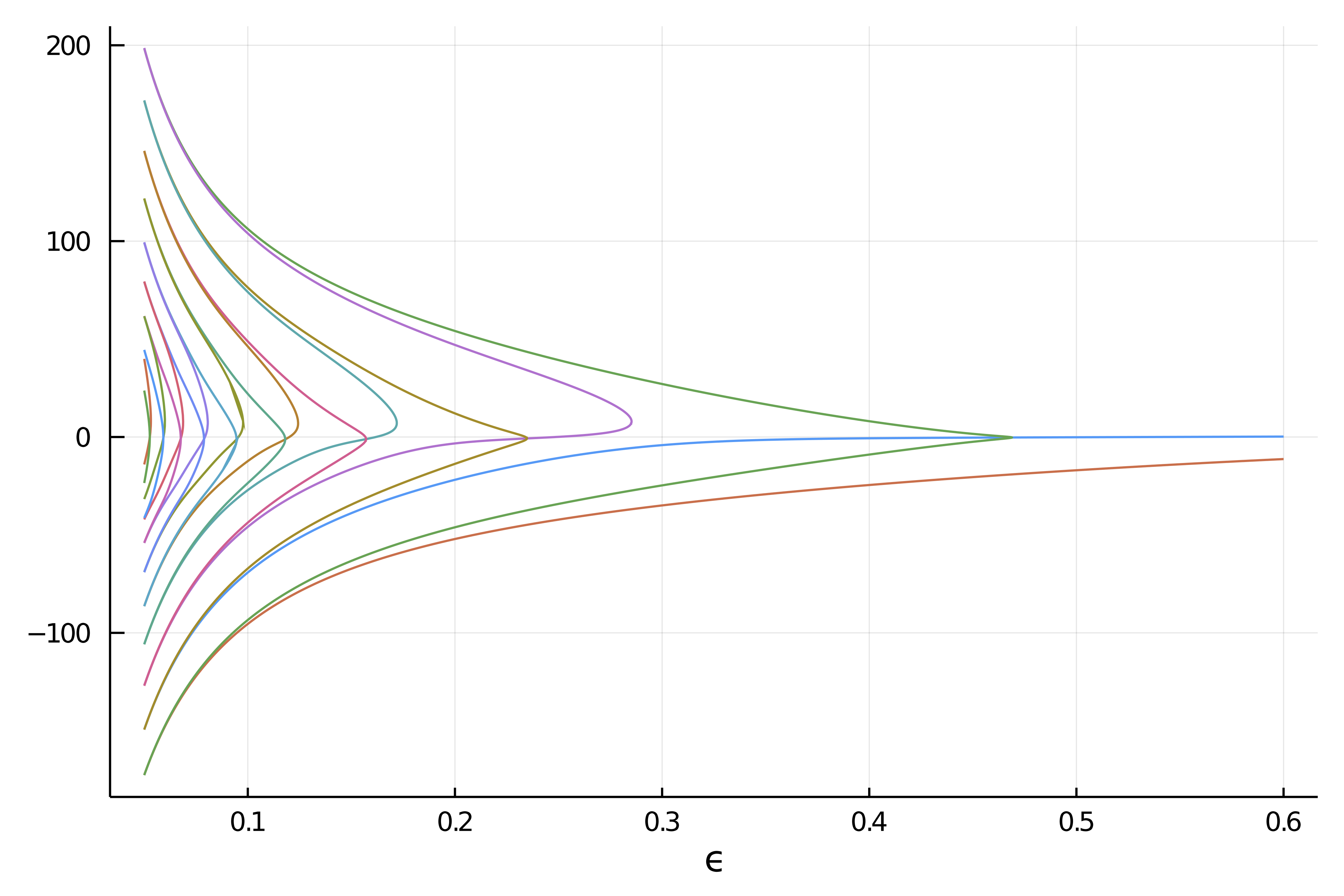
It is a remarkably difficult problem which presents many disconnected branches which are not amenable to the classical continuation methods. We thus use the recently developed deflated continuation method which builds upon the Deflated Newton (see Deflated problems) techniques to find solutions which are different from a set of already known solutions.

We start with some import

using Revise
using LinearAlgebra, SparseArrays, BandedMatrices

using BifurcationKit, Plots
const BK = BifurcationKit

BifurcationKit

and a discretization of the problem

function F_carr(x, p)
	(;ϵ, X, dx) = p
	f = similar(x)
	n = length(x)
	f[1] = x[1]
	f[n] = x[n]
	for i=2:n-1
		f[i] = ϵ^2 * (x[i-1] - 2 * x[i] + x[i+1]) / dx^2 +
			2 * (1 - X[i]^2) * x[i] + x[i]^2-1
	end
	return f
end

function Jac_carr(x, p)
	(;ϵ, X, dx) = p
	n = length(x)
	J = BandedMatrix{Float64}(undef, (n,n), (1,1))
	J[band(-1)] .= ϵ^2/dx^2    									# set the diagonal band
	J[band(1)]  .= ϵ^2/dx^2										# set the super-diagonal band
	J[band(0)]  .= (-2ϵ^2 /dx^2) .+ 2 * (1 .- X.^2) .+ 2 .* x   # set the second super-diagonal band
	J[1, 1] = 1.0
	J[n, n] = 1.0
	J[1, 2] = 0.0
	J[n, n-1] = 0.0
	J
end

Jac_carr (generic function with 1 method)

We can now use Newton to find solutions:

N = 200
X = LinRange(-1,1,N)
dx = X[2] - X[1]
par_car = (ϵ = 0.7, X = X, dx = dx)
sol0 = -(1 .- par_car.X.^2)

recordFromSolution(x, p; k...) = (x[2]-x[1]) * sum(x->x^2, x)

prob = BifurcationProblem(F_carr, zeros(N), par_car, (@optic _.ϵ); J = Jac_carr, record_from_solution = recordFromSolution)

optnew = NewtonPar(tol = 1e-8)
sol = @time BK.solve(prob, Newton(), optnew, normN = norminf)

  0.000147 seconds (84 allocations: 147.641 KiB)

First try with automatic bifurcation diagram

We can start by using our Automatic bifurcation method.

optcont = ContinuationPar(dsmin = 0.001, dsmax = 0.05, ds= -0.01, p_min = 0.05, plot_every_step = 10, newton_options = NewtonPar(tol = 1e-8), max_steps = 300, nev = 40, n_inversion = 4)

diagram = bifurcationdiagram(prob,
    # particular bordered linear solver to use
	# BandedMatrices.
    PALC(bls = BorderingBLS(solver = DefaultLS(), check_precision = false)),
    2,
	optcont)

scene = plot(diagram)

However, this is a bit disappointing as we only find two branches.

Second try with deflated continuation

# deflation operator to hold solutions
deflationOp = DeflationOperator(2, dot, 1.0, [sol.u])

# parameter values for the problem
par_def = @set par_car.ϵ = 0.6

# newton options
optdef = setproperties(optnew; tol = 1e-7, max_iterations = 200)

# function to encode a perturbation of the old solutions
function perturbsol(sol, p, id)
	# we use this sol0 for the boundary conditions
	sol0 = @. exp(-.01/(1-par_car.X^2)^2)
	solp = 0.02*rand(length(sol))
	return sol .+ solp .* sol0
end

# encode the deflated continuation algo
alg = DefCont(deflation_operator = deflationOp, perturb_solution = perturbsol, max_branches = 40)

# call the deflated continuation method
br = @time continuation(
	re_make(prob; params = par_def), alg,
	setproperties(optcont; ds = -0.00021, dsmin=1e-5, max_steps = 20000,
		p_max = 0.7, p_min = 0.05, detect_bifurcation = 0, plot_every_step = 40,
		newton_options = setproperties(optnew; tol = 1e-9, max_iterations = 100, verbose = false));
	normC = norminf,
  verbosity = 0,
	)

plot(br...)

We obtain the following result which is remarkable because it contains many more disconnected branches which we did not find in the first try.