Deflated Continuation

Deflated Continuation

References

Farrell, Patrick E., Casper H. L. Beentjes, and Ásgeir Birkisson. The Computation of Disconnected Bifurcation Diagrams. ArXiv:1603.00809 [Math], March 2, 2016. http://arxiv.org/abs/1603.00809.

Deflated continuation allows to compute branches of solutions to the equation $F(x,p)=0$. It is based on the Deflated Newton (see Deflated problems) algorithm.

See DefCont for more information.

However, unlike the regular continuation method, deflated continuation allows to compute disconnected bifurcation diagrams, something that is impossible for our Automatic Bifurcation diagram computation which is limited to the connected component of the initial point.

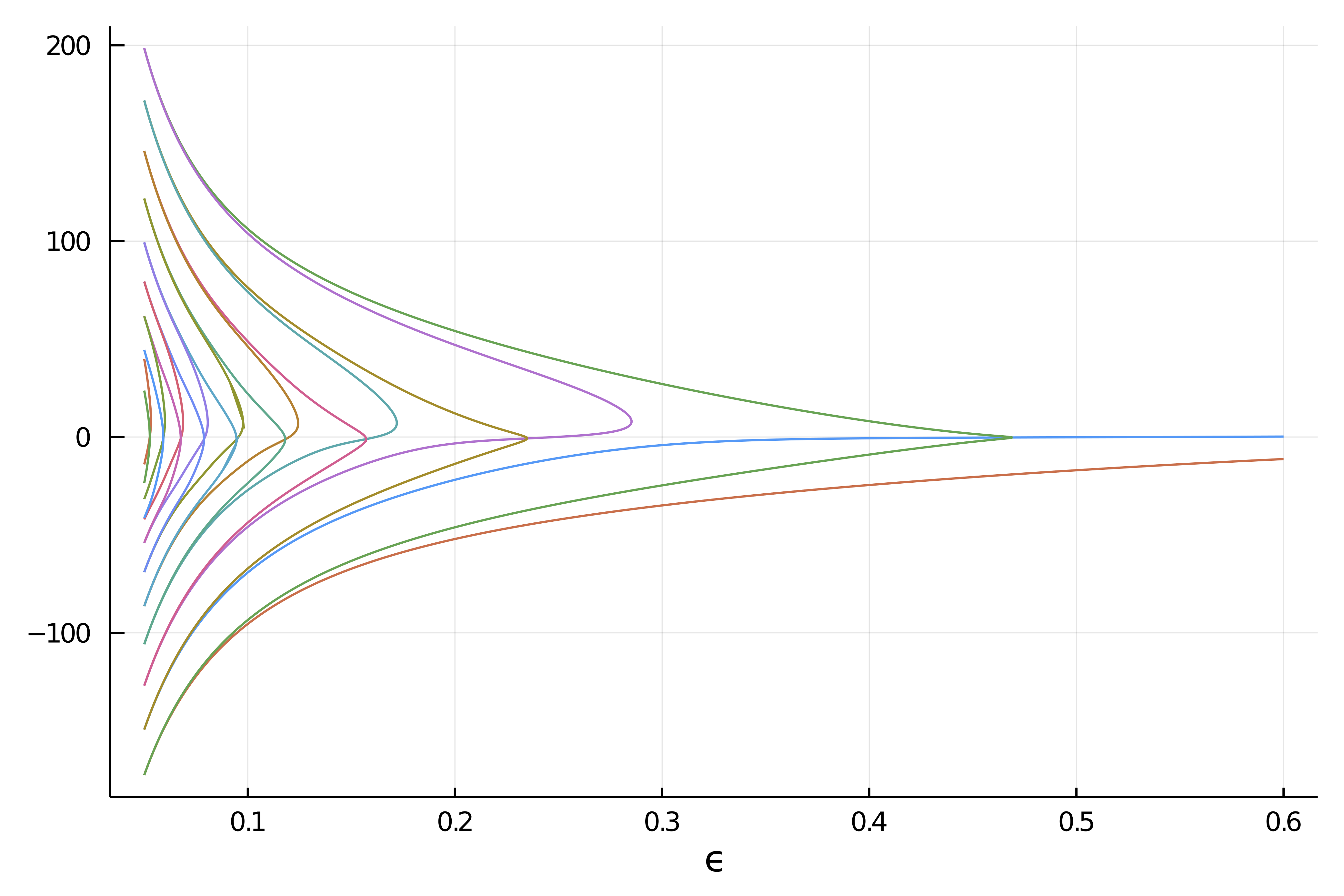
You can find an example of use of the method in Carrier Problem. We reproduce below the result of the computation which shows various disconnected components arising from Fold bifurcations that are found seemingly by the method.

The deflation operator

The deflated continuation is built on the idea of deflating the solutions that have already been found: given known solutions $u^\star_1,\cdots,u^\star_{n}$, one replaces the functional $F$ by the deflated functional

\[G(u;\{u^\star_i\}_i) = F(u)\cdot \prod_{i=1}^n\left(\|u - u^\star_i\|^{-2p} + \alpha\right),\]

where $\|u - u^\star_i\|$ is a norm, $p$ a (positive) power and $\alpha>0$ a shift. The zeros of $G$ away from the $u^\star_i$'s coincide with those of $F$ but the Newton iterations for $G$ are penalized in the neighborhood of the already found solutions $u^\star_i$, hence the name. This product of deflations is implemented in the composite type DeflationOperator; see Deflated problems for its API.

The deflated continuation algorithm then computes, at each value of the parameter, all the solutions which are connected to the ones found at the previous parameter value, together with the solutions lying on disconnected branches which are discovered by starting Newton iterations from perturbed initial guesses. Let us detail this now.

Algorithm

Input: Initial parameter value λmin.Input: Final parameter value λmax > λmin. Input: Step size ∆λ > 0.Input: Nonlinear residual f(u,λ).Input: Deflation operator M(u; u∗).Input: Initial solutions S(λmin) to f(·,λmin).λ ← λminwhile λ < λmax do	F(·) ← f(·,λ+∆λ)                        # Fix the value of λ to solve for.	S(λ+∆λ) ← ∅	for u0 ∈ S(λ) do                         # Continue known branches.		apply Newton’s method to F from initial guess u0.		if solution u∗ found then			S(λ + ∆λ) ← S(λ + ∆λ) ∪ {u∗}     # Record success.			F(·) ← M(·;u∗)F(·)               # Deflate solution.		end	end	for u0 ∈ S(λ) do                         # Seek new (disconnected) branches.		success ← true		while success do			apply Newton’s method to F from initial guess u0.			if solution u∗ found then         # New branch found.				S(λ + ∆λ) ← S(λ + ∆λ) ∪ {u∗} # Record success.				F(·) ← M(·;u∗)F(·)           # Deflate solution.			else				success ← false			end		end	end	λ←λ+∆λendreturn S

Inner loop

The outer loop over u0 ∈ S(λ) (second for) allows to find several disconnected branches. In DefCont, the number of Newton iterations spent searching for new branches is bounded: the maximal number of deflations performed at a given parameter value is max_iter_defop * NewtonPar.max_iterations (default max_iter_defop = 5). This is important because, without this bound, a single parameter value with many solutions could stall the computation.

Tips

The following piece of information is valuable in order to get the algorithm working in various conditions (see also here) especially for small systems (e.g. dim<20):

newton is quite good and it is convenient to limit it otherwise it will be able to bypass the deflation. For example, you can use max_iterations = 10 in NewtonPar
try to limit the newton residual by using the argument callback_newton = BifurcationKit.cbMaxNorm(1e7). This will likely remove the occurrence of ┌ Error: Same solution found for identical parameter value!!
finally, you can try some aggressive shift (here 0.01 in the deflation operator, like DeflationOperator(2, dot, 0.01, [sol]) but use it wisely.

Basic example

We show a quick and simple example of use. Note in particular that the algorithm is able to find the disconnected branch. The starting points are marked with crosses

using BifurcationKit, LinearAlgebra, Plotsconst BK = BifurcationKitk = 2N = 1F(x, p) = @. p * x + x^(k+1)/(k+1) + 0.01Jac_m(x, p) = diagm(0 => p .+ x.^k)# bifurcation problemprob = ODEBifProblem(F, [0.], 0.5, (@optic _), J = Jac_m)# continuation optionsopts = BK.ContinuationPar(ds=0.001, max_steps = 140, newton_options = NewtonPar(tol = 1e-8))# algorithmalg = DefCont(deflation_operator = DeflationOperator(2, .001, [[0.]]), perturb_solution = (x,p,id) -> (x  .+ 0.1 .* rand(length(x))))brdc = continuation(prob, alg,	ContinuationPar(opts, ds = -0.001, max_steps = 800, newton_options = NewtonPar(verbose = false, max_iterations = 6), plot_every_step = 40),	;	plot=false,	callback_newton = BK.cbMaxNorm(1e3) # reject newton step if residual too large	)plot(brdc)