🟡 1d Swift-Hohenberg equation (automatic)

• 🟡 1d Swift-Hohenberg equation (automatic)
• • Exploration of the diagram
  • References

In this tutorial, we will see how to compute automatically the bifurcation diagram of the 1d Swift-Hohenberg equation. This example is treated in pde2path.

\[-(I+\Delta)^2 u+\lambda\cdot u +\nu u^3-u^5 = 0\tag{E}\]

with Dirichlet boundary conditions. We use a Sparse Matrix to express the operator $L_1=(I+\Delta)^2$. We start by loading the packages:

using Reviseusing SparseArraysimport LinearAlgebra: I, normusing BifurcationKitusing Plotsconst BK = BifurcationKitBK.set_plot_backend!(BK.BK_Plots()) # hide

We then define a discretization of the problem

# discretisationN = 200l = 6.X = -l .+ 2l/N*(0:N-1) |> collecth = X[2]-X[1]# define a normconst _weight = rand(N)normweighted(x) = norm(_weight .* x)# boundary conditionΔ = spdiagm(0 => -2ones(N), 1 => ones(N-1), -1 => ones(N-1) ) / h^2L1 = -(I + Δ)^2# functional of the problemfunction R_SH!(out, u, par)	(;λ, ν, L1) = par	out .= L1 * u .+ λ .* u .+ ν .* u.^3 - u.^5end# jacobianJac_sp(u, par) = par.L1 + spdiagm(0 => par.λ .+ 3 .* par.ν .* u.^2 .- 5 .* u.^4)# second derivatived2R(u,p,dx1,dx2) = @. p.ν * 6u*dx1*dx2 - 5*4u^3*dx1*dx2# third derivatived3R(u,p,dx1,dx2,dx3) = @. p.ν * 6dx3*dx1*dx2 - 5*4*3u^2*dx1*dx2*dx3# parameters associated with the equationparSH = (λ = -0.7, ν = 2., L1 = L1)# initial conditionsol0 = zeros(N)# Bifurcation Problemprob = BifurcationProblem(R_SH!, sol0, parSH, (@optic _.λ); J = Jac_sp,	record_from_solution = (x, p; k...) -> (n2 = norm(x), nw = normweighted(x), s = sum(x), s2 = x[end ÷ 2], s4 = x[end ÷ 4], s5 = x[end ÷ 5]),	plot_solution = (x, p;kwargs...)->(plot!(X, x; ylabel="solution", label="", kwargs...)))

We then choose the parameters for continuation with precise detection of bifurcation points by bisection:

opts = ContinuationPar(dsmin = 0.0001, dsmax = 0.01, ds = 0.01, p_max = 1.,	newton_options = NewtonPar(max_iterations = 30, tol = 1e-8),	max_steps = 300, plot_every_step = 40,	n_inversion = 4, tol_bisection_eigenvalue = 1e-17, dsmin_bisection = 1e-7)

Before we continue, it is useful to define a callback (see continuation) for newton to avoid spurious branch switching. It is not strictly necessary for what follows.

function cb(state; kwargs...)	_x = get(kwargs, :z0, nothing)	fromNewton = get(kwargs, :fromNewton, false)	if ~fromNewton		# if the residual is too large or if the parameter jump		# is too big, abort continuation step		return norm(_x.u - state.x) < 20.5 && abs(_x.p - state.p) < 0.05	end	trueend

Next, we specify the arguments to be used during continuation, such as plotting function, tangent predictors, callbacks...

args = (verbosity = 0,	plot = true,	callback_newton = cb, halfbranch = true,	)

Depending on the level of recursion in the bifurcation diagram, we change a bit the options as follows

function optrec(x, p, l; opt = opts)	level =  l	if level <= 2		return setproperties(opt; max_steps = 300,			nev = N, detect_loop = false)	else		return setproperties(opt; max_steps = 250,			nev = N, detect_loop = true)	endend

We are now in position to compute the bifurcation diagram

diagram = @time bifurcationdiagram(re_make(prob, params = @set parSH.λ = -0.1),	PALC(),	# here we specify a maximum branching level of 4	4, optrec; args...)

After ~700s, you can plot the result

plot(diagram;  plotfold = false,  	markersize = 2, putspecialptlegend = false, xlims=(-1,1), label = "")title!("#branches = $(size(diagram))")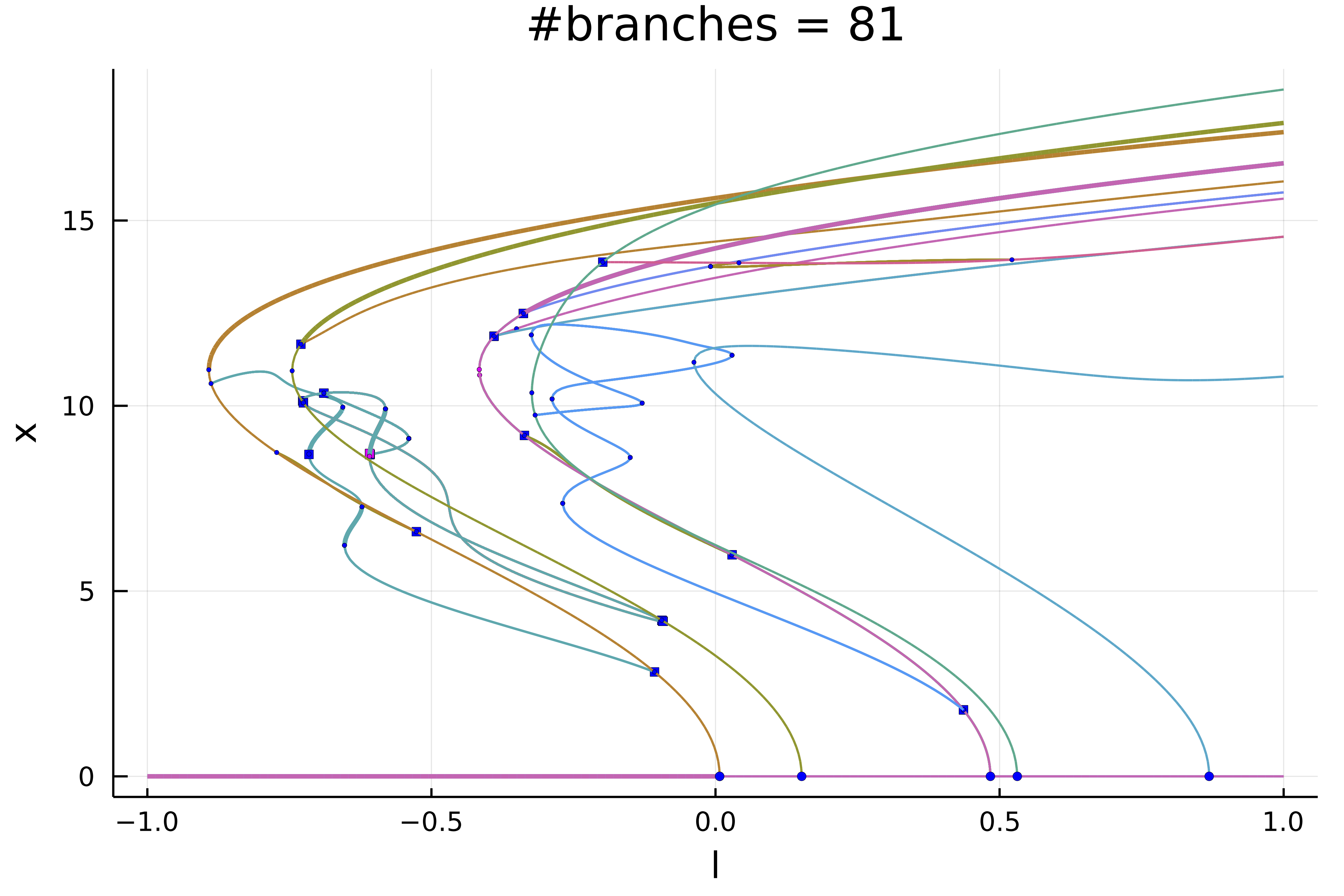

Et voilà!

Exploration of the diagram

The bifurcation diagram diagram is stored as tree:

julia> diagram[Bifurcation diagram] ┌─ From 0-th bifurcation point. ├─ Children number: 5 └─ Root (recursion level 1)      ┌─ Number of points: 82      ├─ Branch of EquilibriumCont      ├─ Type of vectors: Vector{Float64}      ├─ Parameter l starts at -0.1, ends at 1.0      ├─ Algo: PALC      └─ Special points:If `br` is the name of the branch,ind_ev = index of the bifurcating eigenvalue e.g. `br.eig[idx].eigenvals[ind_ev]`- #  1,       bp at λ ≈ +0.00739184 ∈ (+0.00694990, +0.00739184), |δp|=4e-04, [converged], δ = ( 1,  0), step =   8, eigenelements in eig[  9], ind_ev =   1- #  2,       bp at λ ≈ +0.15163058 ∈ (+0.15157533, +0.15163058), |δp|=6e-05, [converged], δ = ( 1,  0), step =  19, eigenelements in eig[ 20], ind_ev =   2- #  3,       bp at λ ≈ +0.48386330 ∈ (+0.48386287, +0.48386330), |δp|=4e-07, [converged], δ = ( 1,  0), step =  43, eigenelements in eig[ 44], ind_ev =   3- #  4,       bp at λ ≈ +0.53115107 ∈ (+0.53070912, +0.53115107), |δp|=4e-04, [converged], δ = ( 1,  0), step =  47, eigenelements in eig[ 48], ind_ev =   4- #  5,       bp at λ ≈ +0.86889123 ∈ (+0.86887742, +0.86889123), |δp|=1e-05, [converged], δ = ( 1,  0), step =  71, eigenelements in eig[ 72], ind_ev =   5- #  6,  endpoint  at λ ≈ +1.00000000,                                                                      step =  81

We can access the different branches with BK.getBranch(diagram, (1,)). Alternatively, you can plot a specific branch:

plot(diagram; code = (1,), plotfold = false,  markersize = 2, putspecialptlegend = false, xlims=(-1,1))

References